Все, что может запутаться, будет запутано, в том числе и ДНК
Нитки с узлами прикрепляют пуговицы к рубашкам. Узлы на веревках прикрепляют лодки к причалам. Вы можете найти узлы на шнурках, галстуках, лентах и бантах. Но даже без бойскаутов или моряков узлы были бы повсюду.
КАТАЛОГ МОТКОВ. Веревки завязываются самопроизвольно, когда их складывают в коробку. Каждый узел (не совсем белый) сочетается с соответствующим идеализированным узлом (золотой). Raymer/UCSD
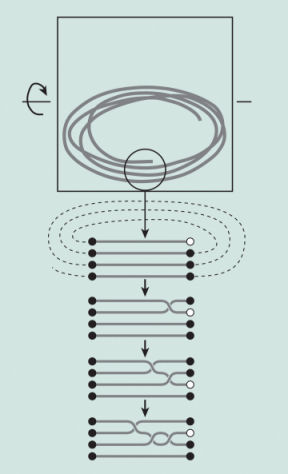
ЗАВЯЗЫВАЮТСЯ УЗЛЫ. Компьютерные модели показали, как смотанная струна в барабанной коробке (вверху) запутывается, когда один из ее концов свободно вращается вокруг других витков. Raymer/PNAS
ДЕЛАЮТ ПЕТЛЮ. На этом снимке, сделанном под электронным микроскопом, видна бактериальная ДНК, завязанная в трилистник, единственный узел, имеющий всего три пересечения. Stasiak/Nature
Назовем это законом узлов Мерфи: если что-то может запутаться, оно это сделает. “Все, что является длинным и гибким, каким-то образом оказывается связанным узлами”, — говорит Эндрю Бельмонте, прикладной математик из Университета штата Пенсильвания в Юниверсити-парке. У Бельмонте есть множество тревожных неофициальных свидетельств. “Это, безусловно, происходит в моем доме, когда речь заходит о шнурах от жалюзи”. Но проблема узлов носит глобальный характер, и любой владелец настольного компьютера может подтвердить это, взглянув на путаницу соединительных кабелей и шнуров питания за письменным столом.
Теперь ученые полагают, что, возможно, им удалось выяснить, как и почему предметы образуют сложные структуры. Биофизики Дориан Раймер и Дуглас Смит, запихивая веревку в коробку, обнаружили, что узлы — даже сложные — образуются на удивление быстро и часто. Сначала бечевка скручивается, а затем ее свободные концы обвиваются вокруг других витков, прокладывая между ними произвольную траекторию. По сути, это превращает витки в косу, образуя узлы, говорят ученые.
Значимость результатов может выходить далеко за рамки объяснения эпидемии запутанных шнуров для жалюзи. Это связано с тем, что спонтанные узлы, по-видимому, широко распространены в природе, особенно в биологических молекулах. Например, наличие узлов может иметь решающее значение для функционирования определенных белков (см. “Узлы в белках”). Кроме того, в ДНК могут случайным образом образовываться узлы, препятствующие дупликации или экспрессии генов — настолько, что живые клетки вырабатывают специальные ферменты, расщепляющие узлы.
Интерес Раймера к узлам возник в ожидании ответа на вопрос. Два года назад он был студентом-старшекурсником и работал в лаборатории Смита в Калифорнийском университете в Сан-Диего (UCSD). Раймеру понравилось посещать занятия по абстрактной теории узлов, которые предлагает математический факультет Калифорнийского университета в Сан-Франциско. Смит сказал ему, что ему следует посещать занятия, только если он сможет найти им практическое применение — какой-нибудь эксперимент с узлами.
Раймер никогда не посещал занятия, но им со Смитом пришла в голову простая идея для эксперимента. Они поместили нитку в кубический контейнер размером с упаковку салфеток. Перевернув коробку 10 раз, “как сушилку для белья”, как выразился Раймер, исследователи надеялись понаблюдать за спонтанным образованием узлов. Им не пришлось долго ждать: узлы образовались сразу. “Первые пару раз это было просто потрясающе”, — говорит Раймер.
Исследователи повторили процедуру более 3000 раз, и узлы образовывались примерно каждый второй раз. Более длинные нити, или более гибкие нити, как правило, завязывались чаще.
Исследователи сделали снимки, планируя собрать точную статистику по типам образующихся узлов. Вскоре Раймер понял, что для того, чтобы разобраться в этом беспорядке, ему все-таки нужно научиться математике узлов.
Готовые инструменты
Теория узлов всерьез зародилась в 1860-х годах под руководством британского физика Уильяма Томсона, позже известного как лорд Кельвин. Кельвин предположил, что атомы различных элементов на самом деле представляют собой различные виды узловатых вихрей в эфире. Он считал, что для того, чтобы заложить основы химии, необходимо классифицировать узлы. В конечном счете физики обнаружили, что эфира не существует. Но математики заинтересовались узлами ради узлов, как частью молодого раздела математики, называемого топологией.
Топология изучает формы. В частности, она изучает свойства форм, на которые не влияют растяжение, перемещение, скручивание или вытягивание — все, что не разрушает объект и не соединяет некоторые его части. Общеизвестным примером является то, что для тополога кофейная кружка — это то же самое, что пончик. В своем воображении вы можете придать кружке форму пончика, и она сохранит свойство иметь отверстие, а именно ручку.
Сфера — это совсем другое. Вы можете сделать из сферы палочку и согнуть ее так, чтобы ее концы соприкасались. Но для превращения этого разомкнутого кольца в пончик потребуется соединить концы, а это запрещено.
В топологии узлом называется любая изогнутая линия, которая замыкается сама на себя, возможно, после прохождения обходного пути в трех измерениях. Круг рассматривается как “тривиальный” узел. Две петли считаются одним и тем же узлом, если вы можете превратить одну в другую с помощью топологических манипуляций, что в данном случае означает все, что не нарушает кривую и не заставляет ее проходить через себя.
Топологически завязанная веревка не является настоящим узлом, пока ее концы свободны. Это потому, что любой из концов всегда может продеться сквозь любое переплетение и развязать узел. Открытая веревка, какой бы сложной она ни была, ничем не отличается от прямого отрезка. (Математики обычно думают, что струны могут растягиваться и быть бесконечно тонкими, поэтому в топологии нет проблемы с тугим узлом.)
Строго говоря, струна в коробке Раймера и Смита никогда не была завязана узлом. Но все равно это был беспорядок. Когда исследователи соединили концы нити, у них получилась замкнутая петля, которую даже математик назвал бы узлом.
Вскоре Раймер понял, что отличить разные узлы друг от друга или распознать, когда два узла одинаковые, — непростая задача. Топологи обычно работают с двумерными рисунками узлов, называемыми проекциями узлов. С разных точек зрения одна и та же кривая будет выглядеть по-разному, как и ее проекции. Лучшими инструментами топологов для распознавания узлов являются алгебраические выражения, называемые узловыми полиномами. Это суммы, кратные переменной, такой как x, возведенные в разные степени. Переменная сама по себе не имеет значения, и вся информация содержится в числах, на которые она умножается. Но xэто упрощает вычисление многочлена узлов, исходя из проекции узла.
Джеймс Александер, математик Принстонского университета, изобрел первый многочлен узлов в 1920-х годах. Два топологически эквивалентных узла всегда будут давать один и тот же многочлен Александера, независимо от того, насколько разными выглядят их проекции. Таким образом, если два узла имеют разные многочлены, они, безусловно, неэквивалентны. Однако обратное неверно: некоторые разные узлы имеют один и тот же многочлен Александера. Это означает, что многочлен Александера не является безотказным способом различения узлов.
В начале 1980-х годов Воан Джонс из Калифорнийского университета в Беркли возродил интерес математиков к узлам, определив новый вид узлового многочлена. Это открытие принесло ему Филдсовскую медаль, самую желанную награду в области математики. Многочлены Джонса различают узлы с большей, если не полной, точностью, чем многочлены Александера. Именно поэтому Раймер выбрал многочлены Джонса для каталогизации своих узлов.
Свяжите землю
Раймер написал компьютерную программу для вычисления полиномов Джонса на основе снимков, которые он делал каждый раз, когда открывал коробку. Программа обнаружила, что на скромной коробке образовалось не менее 120 различных типов узлов. Некоторые из них были довольно сложными.
Самым простым показателем сложности узла является минимальное число пересечений, количество переходов, необходимое для построения простейшей из возможных проекций узла. Для тривиального узла это число равно нулю. Для простейшего истинного узла, трилистника, требуется нарисовать всего три пересечения. Как сообщают Раймер и Смит в журнале Proceedings of National Academy of Sciences от 16 октября, для изготовления нескольких узлов из кувыркающегося ящика потребовалось целых 11 узлов
Раймер говорит, что они со Смитом были удивлены, потому что в предыдущих экспериментах с узлами — физики провели несколько таких экспериментов за последние годы — были обнаружены только самые простые узлы. Например, в 2001 году Бельмонте и его коллеги показали, что подвесная цепочка (не от жалюзи Бельмонте) имеет тенденцию завязываться узлом при встряхивании. В 2006 году команда ученых под руководством физика Йенса Эггерса из Бристольского университета в Англии получила цепочку из шариков, которая образовывала узлы, установив ее на вибрирующую тарелку.
Де Витт Самнерс, прикладной математик из Университета штата Флорида в Таллахасси, говорит, что его не удивило, что в коробке могут образовываться узлы. В ходе компьютерного моделирования математики обнаружили, что случайное движение создает траектории, которые почти всегда переплетаются. Вместе со Стью Уиттингтоном из Университета Торонто Самнерс в 1988 году математически продемонстрировал, что если ждать достаточно долго, то эти случайные блуждания будут запутываться практически в 100 процентах случаев.
Самнерс подозревает, что при более длительном вращении у Раймера и Смита получались бы узлы почти всегда, а не только через раз. “Им следовало бы вращаться дольше”, — говорит Самнерс, чтобы увидеть полный эффект.
С другой стороны, в своей статье Раймер и Смит предлагают теоретическое объяснение беспорядка в их коробке, которое отличается от наиболее распространенного типа случайного блуждания. Поскольку их бечевка имела тенденцию скручиваться независимо от того, образовывались на ней узлы или нет, они создали математическую модель пучка витков в виде ряда параллельных горизонтальных нитей. В ходе компьютерного моделирования Раймер и Смит позволили одной из нитей, представляющей собой один из свободных концов нити, пересечь одну из других нитей в пучке или пройти под ней. После нескольких таких шагов нити переплетались, что часто означало, что веревка в целом завязана узлом.
Эта упрощенная модель не воспроизводила точные результаты эксперимента, но предсказывала, что вероятность образования определенных узлов в течение заданного времени была примерно одинаковой.
Переполненный
Бельмонте называет модель плетения “очень очевидной, но, возможно, не универсальной”, подразумевая, что различные физические явления, вероятно, завязывают узлы по-разному. Например, в бактериальной ДНК одним из способов образования узлов является генетическая рекомбинация. Именно тогда, чтобы облегчить перестановку генов, ферменты разрезают ДНК в двух местах и соединяют концы в другом порядке. Геномы бактерий имеют круглую форму, поэтому при рекомбинации могут образовываться настоящие петли.
В конце 1990-х годов биохимики открыли ферменты, которые, по-видимому, способны обнаруживать наличие узлов в ДНК. Затем ферменты развязывают узлы, разрезая и склеивая их.
Поддержание чистоты ДНК может иметь решающее значение для некоторых из наиболее важных функций клетки. Это связано с тем, что копирование ДНК и считывание содержащейся в ней информации осуществляются другими ферментами, называемыми полимеразами, которые перемещаются вдоль ДНК. “Когда [полимераза] попадает в участок с узлами, она застревает”, — говорит Бельмонте.
Ученые обнаружили похожие ферменты, разрушающие узлы, в клетках, которые имеют хромосомы с открытой цепочкой, например, у человека. Наличие таких ферментов позволяет предположить, что образование узлов может быть проблемой и для хромосом человека. Ученые также обнаружили узлы в митохондриях, клеточных органеллах, которые содержат петлевую ДНК.
Еще одно место, где могут образовываться узлы ДНК, находится внутри вирусов, говорит Анджей Стасяк, специалист по структурной биологии из Университета Лозанны в Швейцарии. Вирусы строят контейнеры, называемые капсид, в которые вирусы плотно упаковывают свою ДНК для перемещения от одной клетки-хозяина к другой. В некоторых вирусах капсид удерживает ДНК при давлении более 60 атмосфер.
Стасиак говорит, что в процессе упаковки, вероятно, происходит свертывание, подобное тому, что наблюдали Раймер и Смит. Их модель «спираль и коса» может помочь объяснить, почему ДНК некоторых вирусов часто оказывается скрученной в узел.
Но даже если результаты Раймера и Смита не будут иметь прямого отношения к молекулам жизни, по словам Бельмонте, они являются “очень хорошим началом” для общего изучения физических узлов. “Теперь мы можем, по крайней мере, задать эти вопросы: Существуют ли универсальные законы вязания узлов?”